10235. Порядок задач

Джону необходимо выполнить n задач. К сожалению, задачи не являются независимыми, выполнение одной задачи возможно только в том случае, если другие задачи уже были выполнены.

Вход. Состоит из нескольких тестов. Каждый тест начинается со строки, содержащей два целых числа: количество задач n (1 ≤ n ≤ 100), пронумерованных от 1 до n, и количество m отношений между задачами. Далее идут m строк с двумя целыми числами i и j, обозначающими тот факт, что задача i должна выполняться перед задачей j.

Тест для которого n = m = 0 не обрабатывается и завершает входные данные.

Выход. Для каждого теста выведите строку с n целыми числами – список задач в возможном порядке их выполнения.

Пример входа	Пример выхода
6 6 1 2 3 2 4 2 2 5 6 5 4 6 3 1 3 2 0 0	3 1 4 2 6 5 1 3 2

РЕШЕНИЕ

графы – топологическая сортировка

Анализ алгоритма

В задаче следует совершить топологическую сортировку вершин ориентированного графа.

Пример

Рассмотрим графы, представленные в примере.

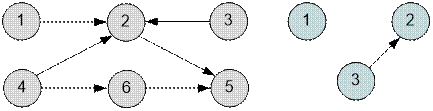
Возможные топологические сортировки для первого графа:

· 3, 1, 4, 2, 6, 5;

· 1, 3, 4, 6, 2, 5;

· 4, 1, 6, 3, 2, 5;

Реализация алгоритма

Объявим матрицу смежности графа g и рабочие массивы used и top.

#define MAX 101

int g[MAX][MAX], used[MAX];

vector<int> top;

Функция dfs совершает поиск в глубину из вершины v. По завершению обработки вершины v (когда она становится черной) заносим ее в массив top.

void dfs(int v)

{

used[v] = 1;

for (int i = 1; i <= n; i++)

if (g[v][i] && !used[i]) dfs(i);

top.push_back(v);

}

Основная часть программы. Обрабатываем несколько тестов.

while (scanf("%d %d", &n, &m), n + m > 0)

{

memset(g, 0, sizeof(g));

Читаем входной граф.

for (i = 0; i < m; i++)

{

scanf("%d %d", &a, &b);

g[a][b] = 1;

}

Инициализируем массивы перед обработкой очередного тесста.

memset(used, 0, sizeof(used));

top.clear();

Запускаем поиск в глубину на ориентированном графе.

for (i = 1; i <= n; i++)

if (!used[i]) dfs(i);

Выводим топологический порядок вершин.

for (i = top.size() - 1; i >= 0; i--)

printf("%d ", top[i]);

printf("\n");

}

Java реализация

import java.util.*;

public class Main

{

static int g[][], used[];

static ArrayList<Integer> top = new ArrayList<Integer>();

static int n, m;

static void dfs(int v)

{

used[v] = 1;

for (int i = 1; i <= n; i++)

if (g[v][i] == 1 && used[i] == 0) dfs(i);

top.add(v);

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

while(con.hasNextInt())

{

n = con.nextInt();

m = con.nextInt();

if (n + m == 0) break;

used = new int[n+1];

g = new int[n+1][n+1];

for (int i = 0; i < m; i++)

{

int a = con.nextInt();

int b = con.nextInt();

g[a][b] = 1;

}

top.clear();

for(int i = 1; i <= n; i++)

if (used[i] == 0) dfs(i);

for(int i = top.size() - 1; i >= 0; i--)

System.out.print(top.get(i) + " ");

System.out.println();

}

con.close();

}

}